Theorems on the Roots of Polynomial Equations

Division Algorithm:

If p(x) and d(x) are any two nonconstant polynomials then there are unique
polynomials q(x) and R(x) such that
p(x) = d(x) q(x) + R(x)
where R(x) is either zero or it is of lower degree than d(x).

Remainder Theorem: If the polynomial p(x) is divided by (x – r) then the constant remainder R
is given by R = p (r).

Factor Theorem: The number c is a solution of the polynomial equation p (x) = 0
if and only if p (x) has (x – c) as a factor.

Complete Factorization Theorem:
If
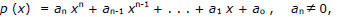
then there are n numbers: 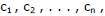not necessarily distinct,
such that

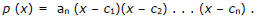
The c_i‘s are the zeros of p(x) and they may be either real or complex
numbers. The complex zeros always occur in conjugate pairs whenever
all coefficients of p (x) are real numbers.

Fundamental Theorem of Algebra:
Every nonconstant polynomial has at least one (real or complex) zero.

Real Factors Theorem:
Any polynomial with real coefficients can be factored into a product of linear
and quadratic polynomials having real coefficients, where the quadratic
polynomials have no real zeros.

Rational Roots Theorem:
Let

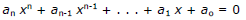
have all integral coefficients. If c/d is a rational solution, in reduced form,
then c divides a_o exactly and d divides a_n exactly.

Descartes’s Rule of Signs:
Suppose that p(x) is a polynomial with real coefficients and with terms written
in descending powers of the variable. Then
(i) the number of positive roots to p(x)=0 is either equal to N: the number
of variations in sign in the coefficients of p(x), or else it is less than N by
an even integer.
(ii) the number of negative roots to p(x)=0 is either equal to M: the number
of variations in sign in the coefficients of p(–x), or else it is less than M by
an even integer.

Upper and Lower Bound Theorem for Real Roots:
Suppose the polynomial:

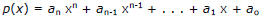
has all real coefficients and a_n>0. Then
(i) the positive number B is an upper bound on the real roots to p(x)=0 if

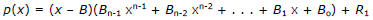
and the numbers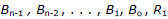 are all nonnegative.
(ii) the negative number b is a lower bound on the real roots to p(x)=0 if

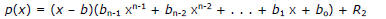
and the sequence of numbers 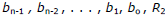are alternately
nonpositive and nonnegative or vice versa.

Location Theorem: If p(x) is a polynomial with real coefficients and a,b are real numbers with
a < b and p(a) and p(b) have opposite sign then there exists at least one
number c such that a < c < b and p(c) = 0.