Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Review division factoring and Root Finding

(This is a brush-up from last semester.)

The division algorithm allows us to write any two
polynomials f(x) and p(x) ≠ 0 uniquely in the form
f(x) = p(x) q(x)+r(x), where q(x) is called the quo-
tient and r(x) is called the remainder.

In lecture we used the division algorithm to show that
factoring is the same as root- nding. In particular, the
remainder theorem tells you that f(c) is the remainder
when you divide f(x) by (x-c). (To see this, write
f(x) = (x-c) q(x) + r. Then f(c) = r.)

Problems.

1. Constructing a polynomial with given roots.

Construct a polynomial with real coefficients that
has exactly the given zeros and degree.

(a) 3-4i, degree 2
(b) 3-4i, 7, degree 3
(c) 3-4i, 7, degree 4

2. Rational roots.

Completely factor the following polynomials.
HINT: The rational roots theorem and synthetic
division can be a big help.

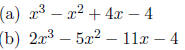
3. Complex arithmetic.

Let z₁ = 2 cis (150°) and z₂ = 3 cis (-60°). Find:

a) z₁ and z₂ in a + bi form
(b) z₂/z₁
(c) z₂-z₁

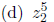
(e) All solutions z to z^2 = z₁.

4. Derivative of a polynomial with a root of multiplicity greater than 1.

Have each person in your group invent a polynomial p that has a root of multiplicity 2. Now
differentiate it to get the polynomial p'. Factor p'. Do you notice a common pattern? Do you think
that this happens in general? Can you prove it?

5. Factoring a quadratic by depressing it.

Suppose you want to factor a quadratic polynomial, i.e. a polynomial of the form Ax^2+Bx+C.
If you divide by A, you will get an equation of the form p = x^2 +βx + γ. We wish to put this
equation in the "depressed" form y^2 + c. To accomplish this, substitute x = y-α and expand
out to get an equation of the form y^2 + by + c. What should α be in order to make the y-term
zero? Choose this α, solve for x, and expand your solution in terms of the original parameters of the
quadratic polynomial (A,B, and C). Do you get a familiar formula?

6. Factoring cubics part I: depressing a cubic.

Ever wonder how to get a general formula for the factors of a cubic polynomial? Begin with a general cubic,

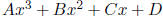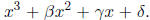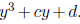Divide by A to get a cubic of the form We wish to put this equation in the "depressed" form The trick is to make a substitution of the form x = y-α .What should α be in order to make the y^2 term zero?

7. Factoring cubics part II: solving a depressed cubic.

Suppose you are trying to factor a depressed cubic,
p = y^3 + cy + d. So you are trying to solve
the equation y^3 +cy +d = 0. The trick is to look
for a solution of the form y = s-t. Plug this in.
Show that we've got a solution if:

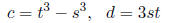
So if we can solve this system for s and t in terms
of c and d, we're done. Do you see how to solve
it?

8. Factoring cubics part III: try an example!

Now let's do an example. To have a nice example
to test out our method, let's make up a cubic
where we already know the roots. I don't know,
how about p(x) = (x-3)(x^2 +1)? Or maybe you
would prefer real roots, e.g. p(x) = (x-5)(x +
1)(x + 4)? Multiply out the factored polynomial
that you pick and then use the methods in the
previous two sections to factor it. Does it work?

You also might try starting with a random depressed
cubic, such as p(x) = x^3-3x + 1. Compute the roots.
Then find the zeros by graphing or using Newton's method.
Do your answers agree?

9. Factoring a quartic.

To factor a quartic equation, first figure out a
substitution that \depresses" it (i.e. gets rid of
the cube term). Then assume that you can write
it as a product of quadratic polynomials with
generic coefficients. Multiply the quadratics to
get a quartic and equate the coefficients with the
coefficients of the depressed quartic. This gives
a system of equations which, with some strategic
elimination of variables, you can reduce to the
problem of finding the roots of a cubic.

10. Factoring a quintic.

Show that it is impossible to represent the roots
of the polynomial f(x) = x^5-x-1 using addition,
subtraction, multiplication, division, or extraction
of roots. Note that this result shows that
it is impossible to find a general formula for the
roots of a polynomial of degree 5 or higher. (Hint:
read up on Galois theory! :)