SYNTHETIC DIVISION AND BOUNDS ON ROOTS

1. Introduction

I screwed up badly when it came to the section on upper and lower bounds of
zeros of polynomials. I apologize profusely for that.

The root of the problem is that I did not define synthetic division correctly,
although what we did do in synthetic division was valid. Synthetic division is not
for me a difficult concept so I really don’t have a good reason for messing it up.
The bad reason is that I have rarely used synthetic division in my career. That is
not to say that it is a useless concept- far from it- just that I’ve not needed it.

I think that once I worked out my mistake, I was able to fix the issue with
synthetic division with relatively little fuss. However, I will include a section on it
here, and then discuss in some detail the issue of bounds on zeroes.

2. Synthetic Division

The method of synthetic division applies only when we divide a non-constant
polynomial, P(x), by an expression of the form x+a. It is best illustrated with an
example.
Example 1. Divide

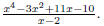
Using long division, we get:

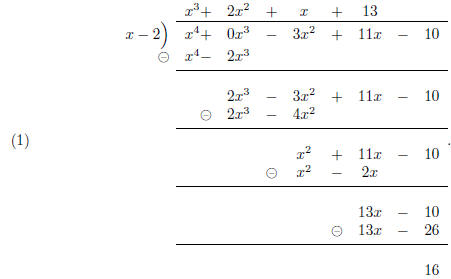
Hence,

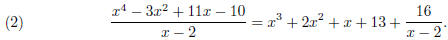
In class, I showed how one can obtain the coefficients with rather less work. It
goes like this:

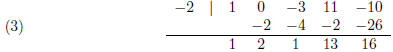
The entries in the first row are the coefficients of the degree 4 polynomial in the
numerator of our original expression. In general, they are the coefficients of P. The
term before the vertical bar is the constant term in the divisor, x − 2. In the more
general situation when we divide by x + a, it is a.

The first entry in the last row is the leading coefficient in P. To obtain the first
entry in the second row, we multiply a by the leading coefficient in P. In general,
an entry in the second row is the product of a with the entry in the third row from
the previous column, and the third row is obtained by subtracting the second row
from the first row.

The last entry is the third row is the remainder constant. The other entries are
the coefficients of the quotient. The reader can match up the entries in the second
row with where they appear in the long division.

This algorithm will always work provided we are dividing P by something of the
form x+a. The algorithm is a modification of what is known as synthetic division
but it is not synthetic division as it is normally defined.

Here is how the synthetic division calculation of the above example goes:

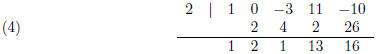
Notice that we changed the sign of the ‘divisor’. As a result, all the signs in the
second row changed. The second row is obtained in the same way as before, but the
third row is obtained by adding the first two rows rather than taking the difference.

This modification is slight, and to a certain extent, the algorithm one uses is a
matter of taste.

For this reason, in this class, I don’t care what method of division that you use
as long as it is valid. If synthetic division is applicable, then so is my algorithm
and vice versa. I would suggest, however, that you do synthetic division rather
than my algorithm, since synthetic division is rather better known and used more
frequently. Moreover, the choice of algorithm affects how several theorems are
stated. Naturally, you will not use either algorithm if you’re divisor is not in the
form x + a.

Remark 2. In fact, synthetic division can be generalized. However, I don’t think
that that is within the scope of the course.

Definition 3. If we are given the expression 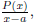and we carry out the division
using synthetic division, we are synthetically dividing by a (not −a.)

In our above example, we synthetically divided by 2.

Theorem 4. Let P be a polynomial with real coefficients. Write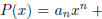
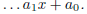Assume a_n > 0. Let d < 0 < c. Using long division, we can write

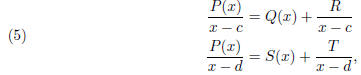
where Q and S are polynomials, and R and T are constants. Then the following
hold:

(i) If the polynomial Q(x)has non-negative coefficients and R ≥ 0, then x > c =>
f(x) ≠ 0. In this situation, c is an upper bound for the real roots of P.

(ii) If the polynomial S(x) has alternating signs, and the constant term in S, s₀,
satisfies the condition 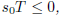then x < d => f(x) ≠ 0. We say that d is a lower
bound for the real roots of P.

This was how I was trying to write the result at the start of the class. Unfortunately,
I was translating from the synthetic division version of the statement in the
book. Since I was using my algorithm, rather than synthetic division, my translation
was flawed. Even if I’d used the standard definition of synthetic division, my
statement would have been flawed, but for rather subtler reasons.

It then didn’t help that I got concerned about the way things were going, and
badly misread the result.

If we compute 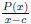using synthetic division, and obtain non-negative entries in
the last row, then c is an upper bound on the zeros of P. Similarly, if 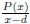  is
computed using synthetic division, and the signs in the last row alternate, d is a
lower bound on the zeros of P.

Let us do the examples that I fumbled in class.

Example 5. Find upper and lower bounds for the real roots of P(x) = x²−2x−4.
We show that 4 is an upper bound and −2 is a lower bound.
For 4, the synthetic division gives:

Since the last line contains only non-negative entries, we conclude that 4 is an upper
bound for the roots. For −2, the synthetic division gives:

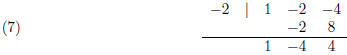
Since the signs in the last row alternate, −2 is a lower bound for the roots.

Example 6. Find upper and lower bounds for the real roots of P(x) = 9x²−6x−1.
We show that 1 is an upper bound and -1 is a lower bound.
For 1, the synthetic division gives:

Since the last line contains only non-negative entries, we conclude that 1 is an upper
bound for the roots. For −1, the synthetic division gives:

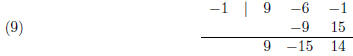
Since the signs in the last row alternate, −1 is a lower bound for the roots.

Example 7. Find upper and lower bounds for the real roots of P(x) = x³ +x+1.
We show that 1 is an upper bound and -1 is a lower bound.
For 1, the synthetic division gives:

For −1, the synthetic division gives:

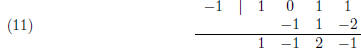
The last lines in both divisions give us the desired result.

I may (and probably will) still grade homework problems where you are asked
to find upper and lower bounds of roots. However, I will not examine you on it.