Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Square Roots and Radical Expressions

CHAPTER 8

Section 8.1: Introduction to Square Roots and Radical Expressions

In this chapter we will learn how to work with radical expressions such as square
roots. A good background in this type of algebra will help us a great deal as we
work with solving polynomial equations that cannot be factored. We will learn
how to do this in chapter 9.

In general the square root of any positive number has two solutions: a positive
solution and a negative solution. But, by convention, when a radical expression is
presented by itself (that is not part of an equation) then we take only the positive
solution and discard the negative solution. This positive answer is called the
‘principle value’. The reason why this is done is related to the mathematics of
functions and is not covered in this course. On the other hand, when radicals are
presented as part of an equation then there may be two solutions.

A. A Square Root: The square root of a number “x” is a number “y” such
that y² = x . Some examples of square roots are as follows:

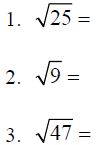
B. Radical Expressions: A radical expression is an algebraic expression that
contains at least one radical sign. Some examples are as follows:

Note that the expression under the radical is called the “radicand”

C. Irrational Numbers: Irrational numbers are numbers that cannot be
written as fractions with integers in the numerator and denominator, or
decimals that terminate or repeat. One of the most famous irrational
numbers is “π ”. “Pi” is the ratio of the circumference of a circle to its
diameter. In this chapter, most of the irrational numbers we will come
across will be square roots of numbers that are not perfect squares.
Identify the following as rational or irrational numbers.

D. Square roots and “Absolute Value”:
For any real number “A”,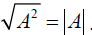 Copy an example from your
instructor that illustrates why the absolute value must be used in this type
of situation:

E. Simplifying rational expressions containing variables: Work through the
following examples: Assume all variables represent non-negative values.

F. Approximating square roots that are irrational: (Use you calculators to
give an approximation to the following square roots that are not rational.
Round each to the nearest hundredth)

Note: Please understand the difference between simplifying a square
root and approximating a square root. What you just did in the three
problems above was approximation, not simplification!

Section 8.2: Multiplying and Simplifying Radical Expressions

Not all square roots are square roots for perfect squares as you saw in the last
section. In this section you will learn how to simplify non-perfect square roots
without approximating them.

A. Multiplying Square Roots: The following is the rule for multiplying
square roots.

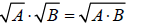(Note that the opposite is true as well)
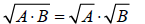(These rules will serve us well)

B. Multiply the following square roots but do not simplify at this time:

C. Simplifying a radical expression: When you want to simplify a radical
that is not a perfect square you will factor it into a special product.
Record what you instructor shows you about this important skill.

D. Simplify the following examples:

E. Multiply the following radical expressions and then simplify:

Section 8.3: Quotients Involving Square Roots

A. We have already learned to simplify radicals in sections 8.1 and 8.2. In this
section we will learn how to remove radicals from the denominator of a
fraction.

1. Removing the radical from the denominator sometimes makes the
expression easier to evaluate.

a. Estimate the following:

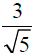
b. Rationalize the denominator: (This means that we will remove the
radical, or irrational number from the denominator of the fraction).

c. Now estimate the result from “b” above:

B. The Quotient Rule for Square Roots:

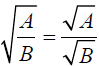The opposite of this is true as well: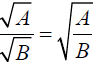

We will use these rules to help us simplify radical expressions that
involve quotients: Work through the examples below to find out how.

C. Note the following:

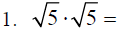
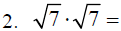
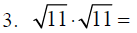
D. Rationalize the denominator or simplify each of the following expressions.

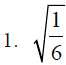
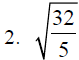
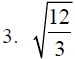
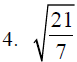
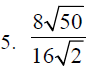
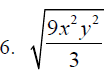
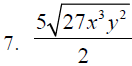
Section 8.4: More Operations with Radicals

Adding radical expression is very similar to adding “like terms” in polynomials.

A. Some examples of polynomial addition and subtraction:

1. (2x² + 3x – 5) + (7x² – 6x + 11) =

2. (3x³ – 7x² + 5x – 7) – (6x² – 5x + 4) =

B. Some examples of addition of radical expressions. In these examples the
radicals are treated somewhat like a variable (e.g. x or y) because they cannot
be further simplified.

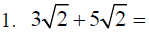
So, just as 3x + 5x = 8x then

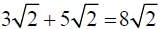
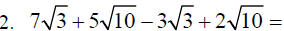
C. Some examples that are a little more complicated. To solve these problems we
must simplify the radial expressions.

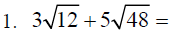
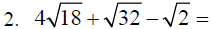
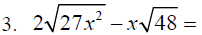
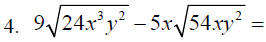
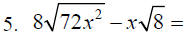
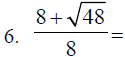
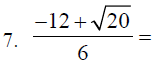
D. More examples that involve multiplication:
Multiply the following expressions and simplify when possible:

Section 8.5: Radical Equations

In this section we will learn how to solve equations that involve Radical
expressions involving square roots. We will accomplish this by using a technique
that involves squaring both sides of the equation with which we are working.
However, we need to be especially careful in this process because we sometimes
arrive at solutions that do not work in our original equation. Note the following
illustration to see what can often happen:

1. Take the following equation: x = 5
2. Square both sides of this equation: _________________
3. Solve this new equation: _________________________
4. How many solutions did the original equation have?
5. How many solutions did the new equation have after we squared both
sides of the equation?
6. What happened?

Obviously squaring can make ‘funny’ things happen to an answer.

A. Solve the following equations and remember to check your results for
“Extraneous” solutions. Before we actually solve anything let’s take a look at
these problems and identify those problems where two answers are likely to
appear.

Indentify the problems below that may have two answers_____________

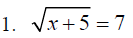
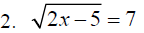
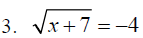
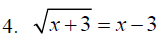
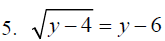
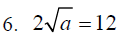
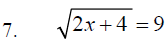
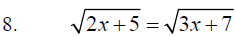
Section 8.6: Applications Using Right Triangles

In this section we will use “Pythagorean Theorem” to solve problems that deal
with right triangles.

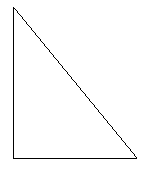
A. Identify the following for the given right triangle:
1. Legs
2. Hypotenuse
3. Right angle

B. Record the formula for the Pythagorean Theorem below:

C. DO THESE PROBLEMS:
1. Find the length of the third side (x). If the answer is not a whole number use
radical notation.

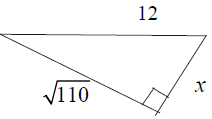
For each of the two problems below, in a right triangle, find the length of the side
not given.

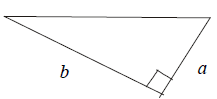
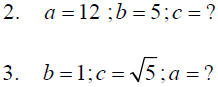
4. MASONRY. Find the length of a diagonal of a square tile with 4 cm sides.

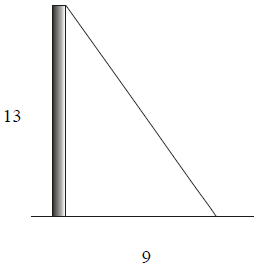
5. How long must a guy wire be to reach from the top of a 13-m telephone pole
to a point on the ground 9 m from the foot of the pole.

6. A soccer field is 100 yd long and 50 yd wide. What is the length of the
diagonal?