Exponents and Roots
 Example 14.
What are the solutions of x3 = 0?
Example 14.
What are the solutions of x3 = 0?
There is only one solution of x3 = 0, namely x = 0. This means that
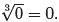
 Example 15. What
are the solutions of x3 = −8?
Example 15. What
are the solutions of x3 = −8?
The graph of the left-hand side of x3 = −8 is the cubic polynomial
shown in
Figure 2. The graph of the right-hand side of x3 = −8 is a
horizontal line located 8
units below the x-axis. The graphs have only one point of intersection, so the
equation
x3 = −8 has exactly one real solution, denoted
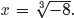 Now since (−2)3 = −8, it
Now since (−2)3 = −8, it
follows that x = −2 is a real solution of x3 = −8. Consequently, the
cube root of −8
is −2, and we write
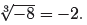
Again, because there is only one real solution of x3
= −8, the notation 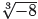 is pronounced
is pronounced
“the cube root of −8.” Note that, unlike the square root of a negative number,
the cube root of a negative number is allowed.
Higher Roots: The previous discussions generalize easily to higher roots,
such as
fourth roots, fifth roots, sixth roots, etc.
Definition 16. Given a real number a and a
positive integer n, an “nth root of
a” is a number x such that xn = a. |
For example, 2 is a 6th root of 64 since 26 = 64, and −3 is a fifth
root of −243 since
(−3)5 = −243.
The case of even roots (i.e., when n is even) closely parallels the case of
square roots.
That’s because when the exponent n is even, the graph of y = xn
closely resembles
that of y = x2. For example, observe the case for fourth roots shown
in
Figures 3(a),
(b), and (c).
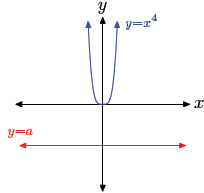
(a) No real solutions. |
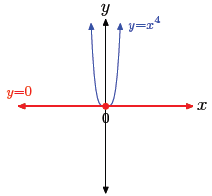
(b) One real solution. |
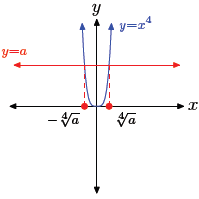
(c) Two real solutions. |
Figure 3. The solutions of x4 = a depend
upon the sign and value of a.
The discussion for even nth roots closely parallels that
presented in the introduction
of square roots, so without further ado, we go straight to the summary.
Summary: Even nth Roots
If n is a positive even integer, then the solutions of xn = a
are called “nth roots
of a.”
• Case I: a < 0. The equation xn = a has no real solutions.
• Case II: a = 0. The equation xn = a has exactly one real
solution, namely
x = 0. Thus, 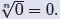
• Case III: a > 0. The equation xn = a has two real
solutions, 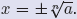 The The
notation 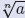 calls for the positive nth
root of a, that is, the positive solution calls for the positive nth
root of a, that is, the positive solution
of xn = a. The notation − 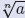 calls for the negative nth root of a, that is, the
calls for the negative nth root of a, that is, the
negative solution of xn = a. |
Likewise, the case of odd roots (i.e., when n is odd)
closely parallels the case of cube
roots. That’s because when the exponent n is odd, the graph of y = xn
closely resembles
that of y = x3. For example, observe the case for fifth roots shown
in
Figure 4.
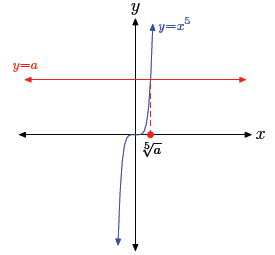
Figure 4. The graph of y = x5 intersects
the graph of y = a in exactly one
place.
The discussion of odd nth roots closely parallels the introduction of cube roots
which
we discussed earlier. So, without further ado, we proceed straight to the
summary.
Summary: Odd nth Roots
If n is a positive odd integer, then the solutions of xn = a
are called the “nth
roots of a.” Whether a is negative, zero, or positive makes no
difference. There is
exactly one real solution of xn = a, denoted
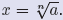 |
Remark 17. The symbols
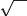 and
and 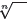 for
square root and nth root, respectively,
for
square root and nth root, respectively,
are also called radicals.
We’ll close this section with a few more examples.
 Example 18.
What are the solutions of x4 = 16?
Example 18.
What are the solutions of x4 = 16?
The graph of the left-hand side of x4 = 16 is the quartic polynomial
shown in
Figure 3(c). The graph of the right-hand side of x4 = 16 is a
horizontal line, located
16 units above the x-axis. The graphs will intersect in two points, so the
equation
x4 = 16 has two real solutions.
The solutions of x4 = 16 are called fourth roots of 16 and are
written 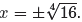
It is extremely important to note the symmetry in Figure 3(c) and note
that we have
two real solutions of x4 = 16, one of which is negative and the other
positive. Hence,
we need two notations, one for the positive fourth root of 16 and one for the
negative
fourth root of 16.
Note that 24 = 16, so x = 2 is the positive real solution of x4
= 16. For this positive
solution, we use the notation
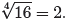
This is pronounced “the positive fourth root of 16 is 2.”
On the other hand, note that (−2)4 = 16, so x = −2 is the negative
real solution
of x4 = 16. For this negative solution, we use the notation

This is pronounced “the negative fourth root of 16 is −2.”
 Example 20.
What are the solutions of x5 = −32?
Example 20.
What are the solutions of x5 = −32?
The graph of the left-hand side of x5 = −32 is the quintic polynomial
pictured in
Figure 4. The graph of the right-hand side of x5 = −32 is a
horizontal line, located
32 units below the x-axis. The graphs have one point of intersection, so the
equation
x5 = −32 has exactly one real solution.
The solutions of x5 = −32 are called “fifth roots of −32.” As shown
from the
graph, there is exactly one real solution of x5 = −32, namely
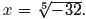 Now since
Now since
(−2)5 = −32, it follows that x = −2 is a solution of x5 =
−32. Consequently, the fifth
root of −32 is −2, and we write
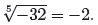
Because there is only one real solution, the notation
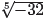 is pronounced “the fifth
is pronounced “the fifth
root of −32.” Again, unlike the square root or fourth root of a negative number,
the
fifth root of a negative number is allowed.
Not all roots simplify to rational numbers. If that were
the case, it would not even
be necessary to implement radical notation. Consider the following example.
 Example 21. Find all real solutions of the equation x2 = 7,
both graphically and
Example 21. Find all real solutions of the equation x2 = 7,
both graphically and
algebraically, and compare your results.
We could easily sketch rough graphs of y = x2 and y = 7 by hand, but
let’s seek a
higher level of accuracy by asking the graphing calculator to handle this task.
• Load the equation y = x2 and y = 7 into Y1 and Y2 in the
calculator’s Y= menu,
respectively. This is shown in Figure 5(a).
• Use the intersect utility on the graphing calculator to find the coordinates
of the
points of intersection. The x-coordinates of these points, shown in Figure 5(b)
and
(c), are the solutions to the equation x2 = 7.
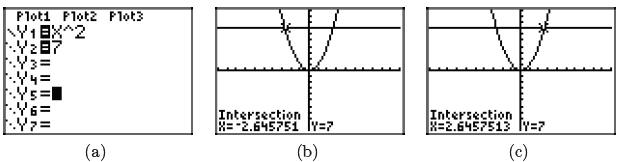
Figure 5. The solutions of x2 = 7 are x ≈
−2.645751 or x ≈ 2.6457513.
Guidelines for Reporting Graphing Calculator Solutions. Recall the
standard
method for reporting graphing calculator results on your homework:
• Copy the image from your viewing window onto your homework paper. Label and
scale each axis with xmin, xmax, ymin, and ymax, then label each graph with its
equation, as shown in Figure 6.
• Drop dashed vertical lines from each point of intersection to the x-axis.
Shade and
label your solutions on the x-axis.
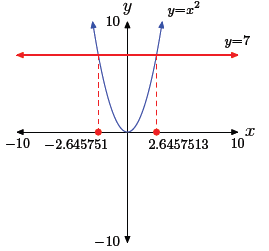
Figure 6. The solutions of x2 = 7 are
x ≈ −2.645751 or x ≈ 2.6457513.
Hence, the approximate solutions are x ≈ −2.645751 or x ≈
2.6457513.
On the other hand, to find analytic solutions of x2 = 7, we simply
take plus or
minus the square root of 7.
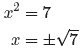
To compare these exact solutions with the approximate
solutions found by using the
graphing calculator, use a calculator to compute
 as shown in Figure 7.
as shown in Figure 7.
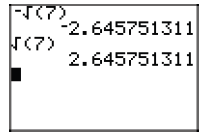
Figure 7. Approximating 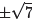 .
.
Note that these approximations of
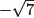 and
and 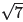 agree quite nicely with the solutions
agree quite nicely with the solutions
found using the graphing calculator’s intersect utility and reported in
Figure 6.
Both 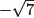 and
and 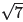 are examples of irrational numbers, that is, numbers that cannot
are examples of irrational numbers, that is, numbers that cannot
be expressed in the form p/q, where p and q are integers.
Rational Exponents
As with the definition of negative and zero exponents, discussed earlier in this
section,
it turns out that rational exponents can be defined in such a way that the Laws
of
Exponents will still apply (and in fact, there’s only one way to do it).
The third law gives us a hint on how to define rational exponents. For example,
suppose that we want to define 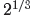 . Then by the
third law,
. Then by the
third law,
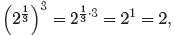
so, by taking cube roots of both sides, we must define
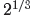 by the formula
by the formula
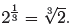
The same argument shows that if n is any odd positive
integer, then 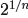 must be
must be
defined by the formula
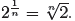
However, for an even integer n, there appears to be a
choice. Suppose that we want
to define 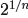 . Then
. Then
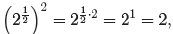
so
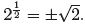
However, the negative choice for the exponent 1/2 leads to
problems, because then
certain expressions are not defined. For example, it would follow from the third
law
that
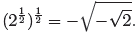
But 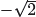 is negative, so
is negative, so
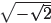 is not defined. Therefore, it only makes
sense to use
is not defined. Therefore, it only makes
sense to use
the positive choice. Thus, for all n, even and odd,
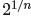 is defined by the formula
is defined by the formula
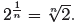
In a similar manner, for a general positive rational
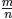 , the third law implies that
, the third law implies that
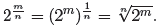
But also,
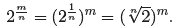
Thus,
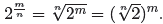
Finally, negative rational exponents are defined in the
usual manner for negative
exponents:
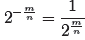
More generally, here is the final general definition. With
this definition, the Laws
of Exponents hold for all rational exponents.
Definition 22. For a positive rational exponent
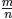 , and b > 0, , and b > 0,

For a negative rational exponent −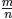 ,
,

|
Remark 25. For b < 0, the same definitions make
sense only when n is odd. For
example 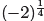 is not defined.
is not defined.
 Example 26. Compute the exact values of
Example 26. Compute the exact values of
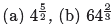 , and
, and 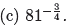
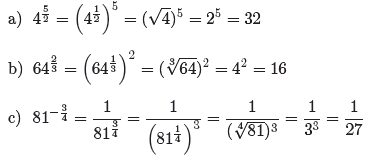
 Example 27.
Simplify the following expressions, and write them in the form xr:
Example 27.
Simplify the following expressions, and write them in the form xr:
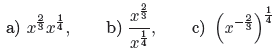
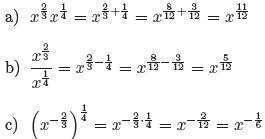
 Example 28. Use
rational exponents to simplify
Example 28. Use
rational exponents to simplify  , and write it
as a single
, and write it
as a single
radical.
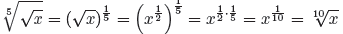
 Example 29. Use a
calculator to approximate
Example 29. Use a
calculator to approximate 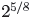 .
.
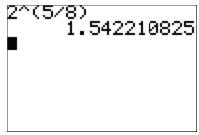
Figure 8.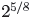 ≈
1.542210825
≈
1.542210825
Irrational Exponents
What about irrational exponents? Is there a way to define numbers like
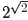 and 3π? It
and 3π? It
turns out that the answer is yes. While a rigorous definition of bs
when s is irrational
is beyond the scope of this book, it’s not hard to see how one could proceed to
find
a value for such a number. For example, if we want to compute the value of
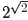 , we
, we
can start with rational approximations for 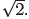 Since
Since
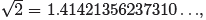 the
the
successive powers
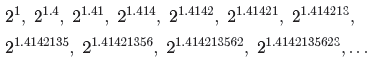
should be closer and closer approximations to the desired
value of
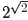 .
.
In fact, using more advanced mathematical theory (ultimately based on the actual
construction of the real number system), it can be shown that these powers
approach
a single real number, and we define
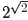 to be that number. Using your calculator, you
to be that number. Using your calculator, you
can observe this convergence and obtain an approximation by computing the powers
above.
Figure 9.
The last value in the table in Figure 9(a) is a correct approximation of
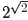 to 10 digits
to 10 digits
of accuracy. Your calculator will obtain this same approximation when you ask it
to
compute
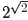 directly (see Figure 9(b)).
directly (see Figure 9(b)).
In a similar manner, bs can be defined for any irrational exponent s
and any b > 0.
Combined with the earlier work in this section, it follows that bs is
defined for every
real exponent s.