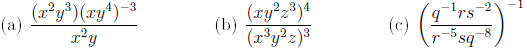Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Exponents and Radicals

Exponential Notation
If a is any real number and n is a positive integer, then the n^th power of a is

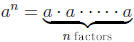
The number a is called the base and n is called the exponent.

Zero and Negative Exponents
If a ≠ 0 is any real number and n is a positive integer, then

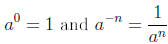
Laws of Exponents

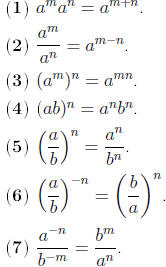
Example 1. Evaluate the expressions

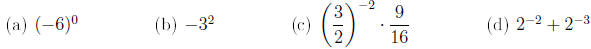
Example 2. Simplify the expressions

Solution.

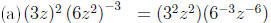	law 4 and 3
	rearrange factors
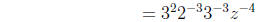	factor 6 and use law 1

	definition of negative exponents

Radicals
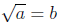means b² = a and b ≥ 0.

Example.
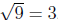, since 3² = 9 and 3 ≥0.
Definition of n^th Root
If n > 1 is a positive integer, then the principal n^th root of a, denoted by 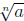is
(1) 0 if a = 0.
(2) the positive number b such that bⁿ = a, if a is positive.
(3) (a) the negative number b such that bⁿ = a, if n is odd and a is negative.
(b) not a real number if n is even and a is positive.

If n is even, we must have a ≥ 0 and b ≥ 0. Complex numbers are needed to define 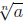if
a < 0 and n is an even positive integer, because when n is even for all real numbers b, we
have bⁿ ≥ 0.
If n = 2 we write 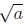instead of .
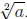Example. 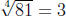since 3³ = 81 and 3 ≥ 0.
Example. 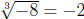since (-2)³ = -8.
Note that 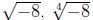are not defined as real numbers.

Properties of n^th Roots

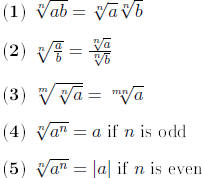
Note that we hav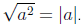e . For example,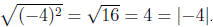

Rational Exponents
Definition. If m and n are integers and n > 1, and if a is a real number such that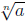
exists, we define
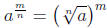or equivalently
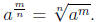
Note that by the definition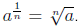
Remark. The laws of exponents hold for rational exponents also.
Example Evaluate the expressions

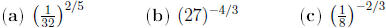
Example Simplify the expressions

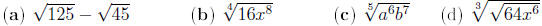
Example Simplify the expression and eliminate any negative exponent(s).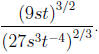

Rationalizing the Denominator
Rationalizing the denominator is to eliminate the radical in a denominator by multiplying
both numerator and denominator by an appropriate expression.
Example.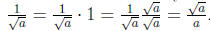
In general, if the denominator is of the form n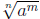 with m < n, then multiplying the
numerator and denominator by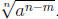
Example Rationalize the denominator

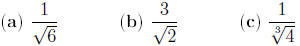
More Examples. Simplify the expressions and eliminate any negative exponent(s)