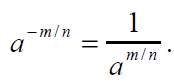Radicals and Rational Exponents

Definition of the Principal Square
Root

• If a is nonnegative real number, the
nonnegative number b such that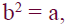
denoted by 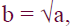,is the principle square
root of a

Square Roots of Perfect Square

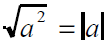
The Product Rule for Square Roots

• If a and b represent nonnegative real
number, then
 

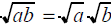and

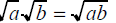
• The square root of product is the product
of the square roots

Text Example

• Simple :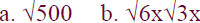

solution :

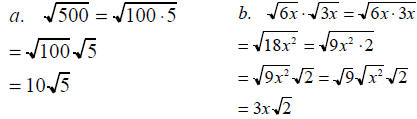
The Quotient Rule for Square Roots

• If a and b does represent nonnegative real
numbers and b does no equal 0, then

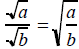and 

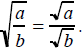
• The square root of quotient  is the
quotient of the square roots

Text Example

• Simple :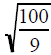

solution :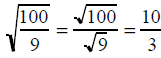

Example

• Perform the indicated operation:

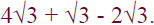
solution :

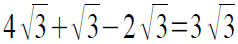
• Perform the indicated operation:

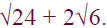
solution :

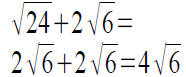
Definition of the Principal nth Root
of a Real Number

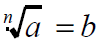means that

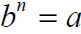
• If n ,the index , is even , then a is
nonnegative (a≥0)and b is also
nonnegative (b≥0).If n is odd ,a and b
can be any real numbers.
 

Finding the nth Roots of Perfect
th Powers

If n is odd ,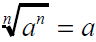
If n is even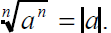

The Product and Quotient Rules
for nth Roots

• For all real numbers ,where the indicated
roots represent real numbers,

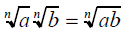and 

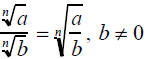
 Definition of Rational Exponents

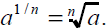
Furthermore

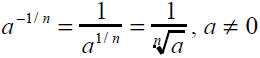
Example

• Simple :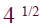

solution:

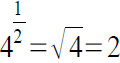
Definition of Rational Exponents

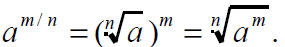
•The exponents m/n consists of two parts :the
denominator n is the root and the numerator
m is  the exponent. Furthermore .