Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Solving Quadratic Equations by Factoring and Extracting Roots

Recall that at the end of chapter 4 we discussed solving polynomial equations. We want to expand upon one particular type of polynomial equation called the quadratic equation.

Definition: Quadratic Equation

A quadratic equation is an equation of the form 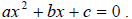. When the equation is written with all terms on one side and zero on the other, the equation is in standard form.

We want to be able to solve all possible quadratic equations. The first method we can use is the method that we learned in chapter 4. That is, by factoring.

In order to solve by factoring we need the following property.

The Zero Product Property

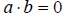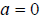If then or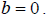

Example 1:

Solve the following equations by factoring.

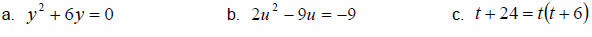
Solution:
a. We first begin by factoring completely. Recall the first step in factoring is factor out the GCF. Then by the zero product property we set each factor to zero and solve. So we get

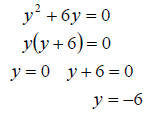
So the solution set is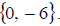

b. In order to solve a quadratic by factoring we first need it in standard form. So we will begin by moving the 9 to get a zero on the one side. Then factor and set each factor to zero. We get

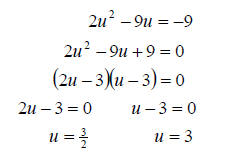
So the solution set is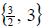

c. Again we need to start by getting the equation into standard form. That means we need to multiply out the parenthesis and move everything to one side. Then we solve by factoring as before.

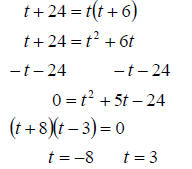
So the solution set is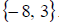

We don’t only want to solve quadratic equations but we also want to be able to get the equation based upon its solutions.

To do so we notice the following: If we solve the equation 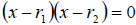we get the solutions of

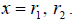
So this tells us that if we start with two solutions, we can simply plug them back into the formula 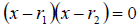to generate the equation.

Example 2:

Write the equation in standard form with integer coefficients that has solutions of the following

Solution:
a. We start by labeling 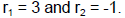Now we insert them into the formula and multiply out to get

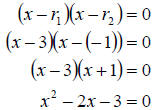
So the equation is .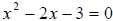

b. Again we label 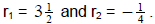We insert them into the formula and multiply as before to get

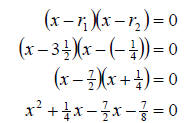
At this point we recall we wanted integer coefficients. Therefore we must clear the fractions. We choose to do this now since it is easier to combine like terms after we clear the fractions. So we multiply both sides by the LCD of 8 and continue

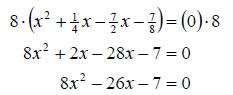
So the equation is .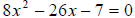

Everything we have done in this section is great, however, we know that not everything factors. So we want to start to build the tools for solving all quadratic equations. The first of these tools is called extracting roots and only works when a quadratic equation is in a very particular form.

First consider the equation 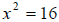. Solving by factoring we get

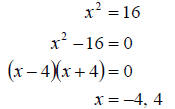
In order to simplify the two answers into one single expression we simply write

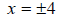
So from this we can see the following

Principle of Extracting Roots

If 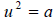then

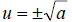
So what this property states is, when we have a squared expression on one side of the equation, we can “square root” both sides to simplify. We simply need to remember to put the 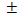in front of the numerical side to show that we have two possible answers.

The real reason for the 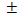symbol goes back to the property that states 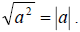For simplicity we omitted the absolute value however, knowing how to solve absolute value equations we would really get

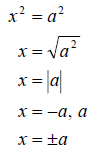
Whichever way you choose to remember it, (either as just a rule or as the absolute value) just make sure that the 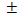is used.

Example 3:
Solve the following.

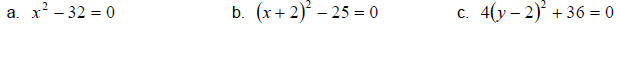
Solution:
a. Since factoring can clearly not solve this equation we will apply the principle of extracting roots. To do this we must first get the x^2 isolated on one side. We then “take the square root of both sides” and attach the 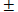symbol.

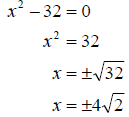
So the solution set is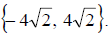

b. Again we need to extract the roots to solve. First we need to isolate the portion of the equation which is squared. Then we extract the roots as follows

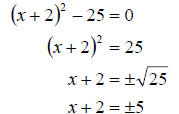
We still need to completely isolate the variable x so we have

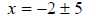
Now, recall the ± represents two possible cases, + and -. So since we can actually calculate –2 + 5 and –2 - 5 we need to split the ± symbol up and finish calculating the solutions. We have

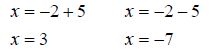
So the solution set is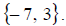

c. Finally, we again use extracting roots to solve.

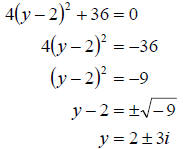
Recall,

So we have two complex number solutions. The solution set is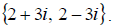

10.1 Exercises

Solve the following equations by factoring.

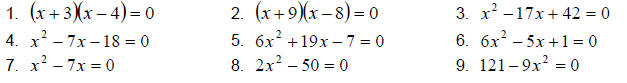
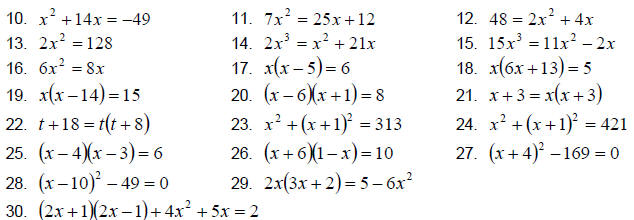
Write the equation in standard form with integer coefficients that has solutions of the following.

Solve the following.