Exponents and Radicals

Solutions to Examples

2.1. Solution:

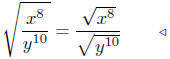	Prop. Rads. #3
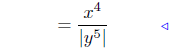	Prop. Rads. #1
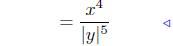	A Prop. Abs. Value #

(S-1)

Example Notes: In equation (S-1), no absolute values were needed for
the x⁴ since x⁴ ≥ 0; however, it is possible for y⁵ to be negative, hence
the absolute values were needed.
Example 2.1.

2.2. Solution:

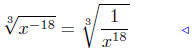	defn of a-n
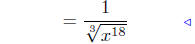	Prop. Rads. #3
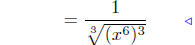	Law Exp. #3
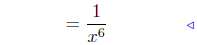	Prop. Rads. #1

Example 2.2.

Important Points

That’s Right! The correct answer is (b).
The square of −3 = (−3)² = (−3)(−3) = 9

First choice or second? If you chose (a) as your first choice, you have
a weakness in this area. Some students erroneously write −3² when
what they really mean is (−3)². A mathematician would interpret the
expression −3² as −(3)(3) = −9; that is the correct interpretation of
the notation −3² is the negative of the number3 squared.

You must be careful about writing −3² when, in reality, you mean
(−3)². You and the one grading your paper might have a difference
in opinion about the meaning of the symbol—guess who wins the
argument.

Therefore, when raising a number that has a negative sign, always
enclose the number, including negative sign, with parentheses. Thus,
cube of the number −2 is (−2)³ = (−2)(−2)(−2) = −8.

Similar comments can be made about symbolic numbers: The cube of
the number −x is (−x)³ not −x³. More on this later.
Important Point

Good Choice! The correct response is ‘n.o.t.’, which means ‘none of
these.’

A common error students make when (trying) to manipulate radicals
is to essentially write (on a test paper, for example)

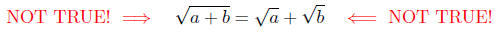
But this is an algebraic blunder! Don’t do that! The root of a sum of
two quantities in not equal to the sum of the roots. A simple example
will illustrate

Symbolic quantities such as a and b represent numbers. Equations you
write involving symbolic quantities must be true when the symbols
are replaced with numbers. To see that the root of a sum is not equal
to the sum of the roots, just give a and b appropriate values.

Take a = 9 and b = 16. Thus,

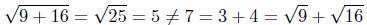
Look at the extreme left and right sides of this nonequation. What
do you see?

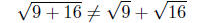
That is,

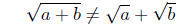
Don’t make this mistake ever again! Important Point

Correct Again! It is not always true that 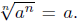Sometimes the
radical 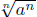equals a and sometimes it doesn’t equal a. Here are some
examples.

Example 1. Situation where 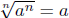is false. Think of a = −1 and
n = 2, then

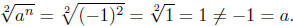
Example 2. Situation where 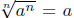is true. Think of a = 1 and
n = 2, then

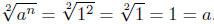
Sometimes it true, sometimes its false. When trying to simplifying a
symbolic expression like 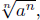it turns out that we need to know the
sign of the number a.

Continue now the discussion following this quiz for a definitive explanation
of how to simplify radicals like 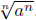. Important Point

Way to go, mate! Because we are taking the square root of x²y, it is
an implicit assumption that x²y ≥ 0. Since x² ≥ 0 regardless of the
value of x, we deduce y ≥ 0.

Now by Law #2 of the Properties of Radicals we have

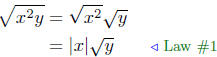Important Point

The original expression was 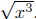from which we deduce that x³ ≥ 0;
hence, x ≥ 0. Thus, |x| = x since x ≥ 0. ’Nuff Said!
Important Point

Solution:

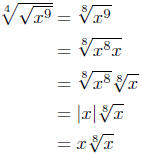
The last step needs some comment. Because we started with the expression
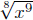we conclude that 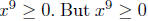implies that x ≥ 0,
because we are dealing with an odd power of x.

Finally, x ≥ 0 implies |x| = x. What was simple!

Awareness of the signs of the quantities is often essential to a successful
simplification. Important Point

Way to go! Convert to exponential notation, reduce fractions, then
return to radical notation.

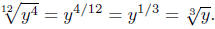
Important Point