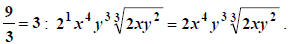Radicals
The Basics
(0) In this discussion we will ONLY deal with REAL
quantities – that is, no Complex Numbers
(1) The index for any radical can only be a positive
integer greater than 1. For such indices, we make these definitions:
| If n is odd,
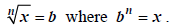 |
If n is even and , x ≥ 0
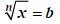 where b ≥ 0 and where b ≥ 0 and
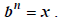 |
For odd indices can be positive, zero or negative and the
resulting 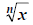 will be positive, zero or negative
respectively. For example,
will be positive, zero or negative
respectively. For example,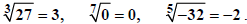 However, for even
indices the radicand MUST be non-negative and the resulting
However, for even
indices the radicand MUST be non-negative and the resulting
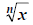 will also be non-negative. For example, but
will also be non-negative. For example, but
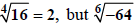 is not defined. (Actually, it can be defined,
but it involves i, and we’ve agreed not to use i here.)
is not defined. (Actually, it can be defined,
but it involves i, and we’ve agreed not to use i here.)
(4) We have another notation for
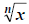 that uses exponents:
that uses exponents:
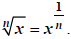 These fractional exponents obey all the laws
of exponents. For example, “when you multiply the bases, you add the exponents”:
These fractional exponents obey all the laws
of exponents. For example, “when you multiply the bases, you add the exponents”: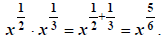 However, we haven’t defined objects like
However, we haven’t defined objects like 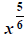 yet
so we won’t push this idea here. So far we’ve only defined the meaning of
fractional exponents if the numerator is 1 (a unit fraction).
yet
so we won’t push this idea here. So far we’ve only defined the meaning of
fractional exponents if the numerator is 1 (a unit fraction).
(5) On your calculator you use parentheses around the
exponent. For example, 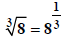 is entered on the
calculator as .
is entered on the
calculator as . 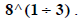 Similarly,
Similarly,
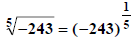 would be entered as
would be entered as
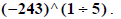
(6) We have the following rule.
| If n is odd,
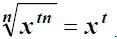 |
If n is even and
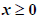 , ,
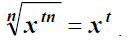 |
These rules make sense if you look at the exponent form:
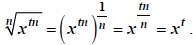 Thus, you can eliminate the radical if the
radicand is an object raised to a power which is a multiple of the index. For
example,
Thus, you can eliminate the radical if the
radicand is an object raised to a power which is a multiple of the index. For
example,
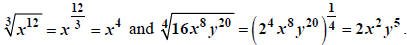
(7) Note: 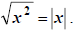 This is
obvious if x is non-negative:
This is
obvious if x is non-negative: 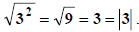 It really
comes into play if x is negative:
It really
comes into play if x is negative: 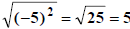 which is
NOT what we started with. In this case
which is
NOT what we started with. In this case 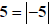 which
is what the rule requires.
which
is what the rule requires.
Some Manipulative Skills
(1) A basic definition:
If m and n are integers with
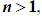 then
then
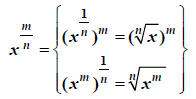
provided 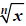 is real.
is real.
We have the option on 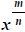 to (a) root first, then power or (b) power first, then root. However, the “root
first, then power” part of the definition is the ONLY WAY we want to do these
things. It is in keeping with the idea of make small before making big that we
saw long ago. So, for example:
to (a) root first, then power or (b) power first, then root. However, the “root
first, then power” part of the definition is the ONLY WAY we want to do these
things. It is in keeping with the idea of make small before making big that we
saw long ago. So, for example:
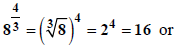
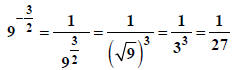
(2) Other manipulations:
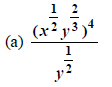 |
mult. & div. only -> put power throughthe product |
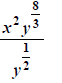 |
divide the bases -> subtract the exponents |
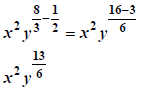 |
|
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
- - - - - - - - - - - - - - - - - - - - -
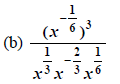 |
mult. & div. only -> flip LAST |
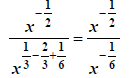 |
divide the basis -> subtract the exponents |
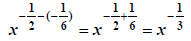 |
now flip |
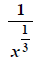 |
|
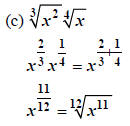 |
indices different -> convert to fractional
exponents |
(3) More rules:
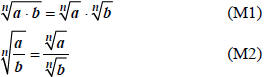
provided at least one 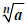 of
of 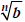 and is real
and is real
Remember:
There is NO RULE for simplifying a radicand that is a sum
or difference:
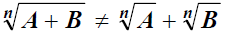
We combine the rules above with the following rule to not
only manipulate but also simplify radicals:
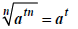 (S)
(S)
provided 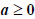 if n is even
if n is even
For example, to simplify
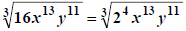 we begin by finding the largest multiples of
3 that do not exceed the given exponents: 3, 12, and 9 respectively in this
case. We “peel these powers off”
we begin by finding the largest multiples of
3 that do not exceed the given exponents: 3, 12, and 9 respectively in this
case. We “peel these powers off” 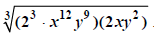 Now, we can
apply (S) along with (M1) all at once after we note that
Now, we can
apply (S) along with (M1) all at once after we note that
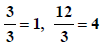 and
and