Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Radicals

Rationalizing the Denominator

(1) The process of eliminating radicals from denominators is called rationalizing the denominator. There are many techniques for doing this depending on the nature of the denominator. We’ll study only two of them. The first of these methods applies when the denominator is just a radical, and it uses the insight gained by having worked with the (S) rule above.

Examples:

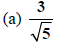
Since this is a square root, we need objects in the radicand that are raised to a
power that is a multiple of 2. We have 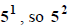is the closest. We can get 512
that by multiplying numerator and denominator by 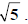I like to think of this as
“multiply by 1 in disguise with radicals”—the old Beatles song!

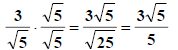
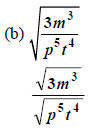
First use (M2).

4 is a multiple of 2, so 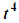is not a worry. The next multiple of 2

past 5 is 6, so we multiply by 1 in disguise with radicals: 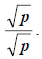While
we’re at it, we’ll simplify the numerator.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

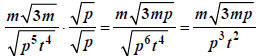
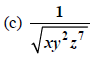
This is getting boring. The current powers are 1, 2, and 7. So
weneed 2, 2, and 8 which we can get by using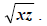

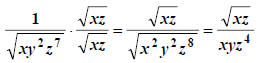
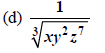
Oh, the same radicand, but a new index. Now we want powers
that are multiples of 3. In this case we want 3, 3, and 9. Thus we use

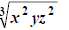
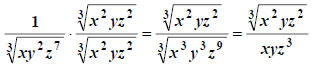
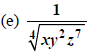
Now the index is 4, so we need the powers 4, 4, and 8.

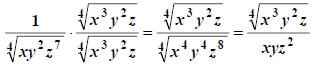
As we see from these last three examples, what we multiply the numerator and denominator by depends both on the radicand and the index.

(2) Before we can introduce the second technique, we need to do some radical arithmetic. The pairs of objects like 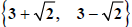and 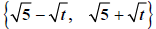are called conjugate pairs. If we apply the special product 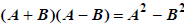to these, we get:

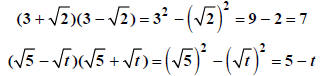
Notice that the radicals vanish in this process. This observation is used to handle fractions whose denominators are one of these types of objects. Some examples follow. NOTE: The above ONLY applies for conjugates involving SQUARE ROOTS – it is not true for cube roots, etc.

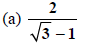Use 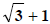and multiply by 1 in disguise with radicals.

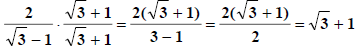
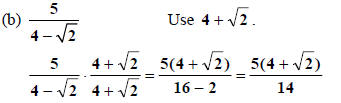
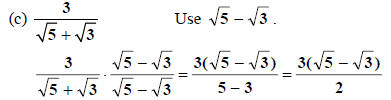
Radical Equations

(1) A radical equation is any equation containing a radical with the variable we want to solve for as part of a radicand. At this level, we will only be interested in square roots – although once you understand the method for square roots, you should be able to extend its basic idea to other indices, but I won’t ask you to do that here.

(2) Solving radical equations (square root ones) is fairly straight forward and the process sounds like the bar tender on the old Love Boat: ISSC.

Isolate a radical
Square both sides of the equation
Solve the resulting equation
Check your solutions

Example 1:

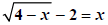	Isolate a radical.
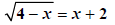	Square both sides.
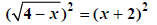	Note: Square both SIDES, not square all terms!!!!
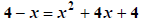	Solve the resulting equation.
	Quadratic -> Make equation to 0
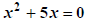	Factor.
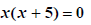	Zero Product Rule.

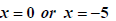But we’re not done just yet! The C in ISSC says Check your solutions. Check them, that is, IN THE ORIGINAL EQUATION 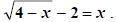Watch very carefully what happens in the following checking process. We substitute each “answer” into the ORIGINAL EQUATION and ask if we do indeed have equality.

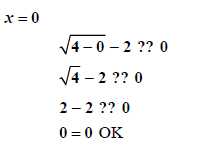
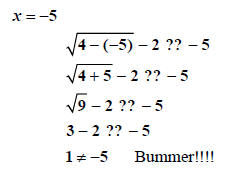
So 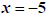does NOT check, and hence it must be tossed out. The only solution is
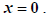
What happened here is that 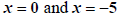are, indeed, solutions to 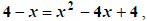the “squared” equation, but only 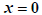is a solution to the original equation. The quantity 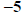is called an extraneous root: a solution to the square of an equation which is NOT a solution to the original equation. This can often happen and hence, along with fractional equations, the technique for solving radical equations requires checking. Unlike the simple checking for zero denominators that was required for fractional equations, the checking here must be complete – substitute into the ORIGINAL EQUATION and verify whether or not the two sides reduce to the same value. In general, anything could happen in this checking process: you might have to throw one or more solutions away (as above), throw them all away (solution set is then 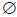), or you may get to keep them all.

Example 2:

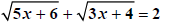	Isolate a radical, say the first one.
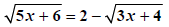	Square both sides.

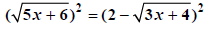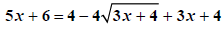	Solve the resulting equation. But this is a radical equation -> ISSC. So Isolate a radical.

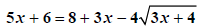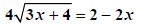	Divide through by to simplify.
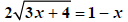	Square both sides.

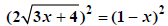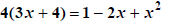	Note the 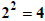up front. Solve the resulting equation.
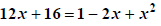	Quadratic -> make equation to 0.
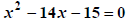	Factor.
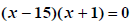	Zero Product Rule
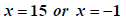	Check.

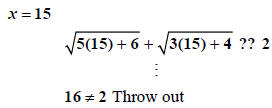
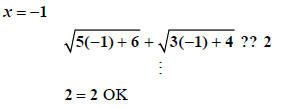
Thus the solution is 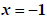.