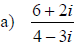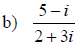Roots, Radicals, and Root Functions

Conditions for a Simplified Radical

1. The radicand has no factor raised to a power greater than or equal to the index.
2. The radicand has no fractions.
3. No denominator contains a radical.
4. Exponents in the radicand and the index of the radical have no common factors, except 1.

Examples: Fully simplify the given radical expressions.

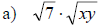
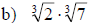
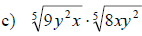
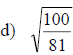
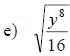
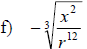
Simplifying Radicals
• Recall that to simplify a square root we look for a number multiplied by itself twice to give us the radicand

• A similar idea holds for all values of the index

• If we cannot find a value multiplied by itself twice to give us the radicand in a square root, we then look for square multiples of the radicand

• If the index was three, we would be looking for cube multiples of the radicands

Examples: Fully simplify the given radical expressions.

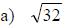
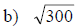
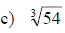
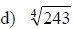
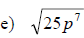
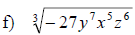
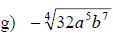
The Pythagorean Relation

• If c is the length of the longest side of a right triangle and a and b are the lengths of the shorter sides, then.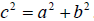

• The longest side is the hypotenuse, and the two shorter sides are the legs of the triangle.

• The hypotenuse if the side opposite the right angle.

Examples: Find the length of the unknown side in the given right triangle.

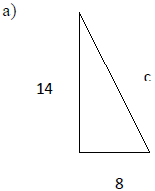
Distance Formula

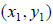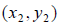• To determine the distance between two points, and on a coordinate plane
 

•

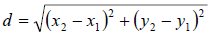
Examples: Find the distance between the pair of given points.

a) (2, -1) & (5, 3)

Section 10.4: Adding and Subtracting Radical Expressions

• When adding and subtracting radical expressions we must have the same index and radicand

• If the radicands are not the same then we try to simplify the radicands so they are the same

Examples: Add or subtract to simplify each radical expression. Assume that all variables represent positive real numbers.

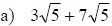
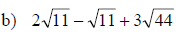
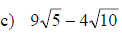
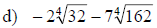
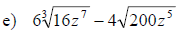
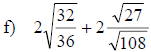
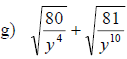
Section 10.5: Multiplying and Dividing Radical Expressions

• When multiplying radical expressions we can use the distributive property

• When multiplying radical expressions with binomials we FOIL

• Recall, when multiplying radical expressions we can only multiply radicals with the same index

Examples: Multiply the radical expressions.

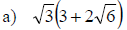
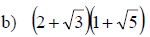
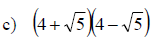
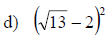
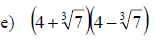
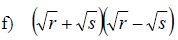
Rationalizing Denominators

• Recall that a radical expression is not fully simplified if radicals are present in the denominator of a fraction

• We use the method of rationalizing denominators to remove the radical from the denominator of a fraction

• Note,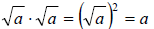

Examples: Rationalize each denominator.

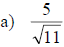
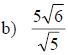
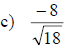
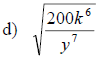
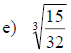
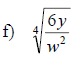
Rationalizing a Binomial Denominator

• Whenever a radical expression has a sum or difference with square root radicals in the denominator, rationalize the denominator by multiplying both the numerator and the denominator by the conjugate of the denominator

• Conjugates have the same terms with opposite signs;

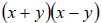
Examples: rational each denominator.

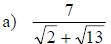
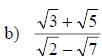
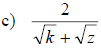
Writing Radical Quotients in Lowest Terms

• Factor the numerator and the denominator

• Divide out any common factors

Examples: Write each quotient in lowest terms.

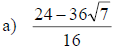
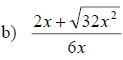
Section 10.6: Solving Equations with Radicals

• We now look at how to solve equations with radical expressions

• We use the following fact to solve these types of equations
-If both sides of an equation are raised to the same power, all solutions of the original equation are also solutions of the new equation

Solving an Equation with Radicals

1. Isolate the radical

2. Apply the power rule

3. Solve the resulting equation

4. Check all solutions in the original equation

Examples: Solve the following equations.

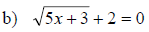
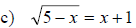
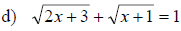
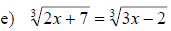
Section 10.7: Complex Numbers

• Recall that the square root of a negative number is a non-real number

• A non-real number is also called a complex number

• We use complex numbers to define square roots of negative numbers

• The imaginary unit i is used to define any square root of a negative real number 1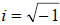 and

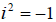
• For any positive real number b,

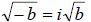
Examples: Write each number as a product of a real number and i

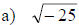
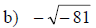
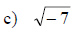
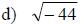
Multiplying and Dividing Square Roots of Negative Numbers

• The product rule and quotient rule only applies to nonnegative radicands

• We must change 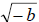to the form 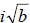before performing multiplication

• Recall that, 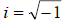and

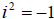
Examples: Multiply or divide as indicated.

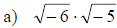
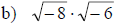
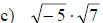
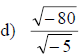
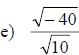
Complex Number

• If a and b are real numbers, then any number of the form

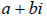
Is called a complex number

• In the complex number, then number a is the real part and is the imaginary part bi

Adding and Subtracting Complex Numbers

• Combine the real parts

• Combine the imaginary parts

Examples: Add or subtract the given expressions as indicated.

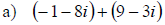
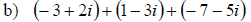
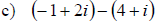
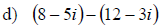
Multiplying Complex Numbers

• We use the distributive property

• FOIL binomials

• Recall that 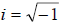and

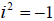
Examples: Multiply the given expressions. Give a fully simplified result.

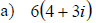
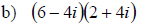
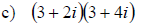
Dividing Complex Numbers

• Multiply the numerator and denominator by the conjugate of the denominator

• Recall that conjugates are of the form

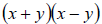
• We multiply by the conjugate to rationalize the denominator

Examples: Find each quotient. State the conjugate that will be used to rationalize the denominator.