Radical Expressions

9.2 Add, Subtract, and Multiply Radical
Expressions

Consider the radical expression 

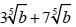
Use the distributive property
to rewrite the expression in
factored form. Then simplify
the expression.

Like Terms & Combining Like Terms
Like terms have identical variable and radical
factors. To combine like terms means to add the
coefficients while leaving the variable and radical
factors unchanged.

To add or subtract radical terms means to combine like terms

Example 1
Perform the indicated operation.

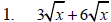
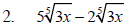
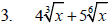
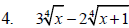
Example 2
Perform the indicated operation.

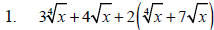
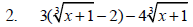
Example 3
Perform the indicated operation.

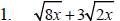
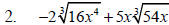
Multiply Radical Expressions

Product Property of Radicals
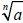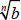If and are real numbers, then .
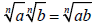Specifically, if n = 2 and a = b, then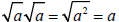

Example 2
Perform the indicated operation.

Example 3
Perform the indicated operation and simplify.

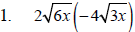
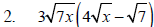
Example 4
Perform the indicated operation and simplify.

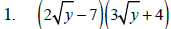
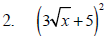
Example 4

Simplify

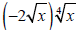
i. Write the expression in
exponential form

ii. Perform the indicated
operation(s)

iii. Write the expression in radical
form

9.3 Rationalizing Denominators and Simplifying
Quotients of Radical Expressions

A simplified radical expression cannot have a radical in the
denominator. The procedure for removing a radical from
the denominator is called rationalizing the denominator.
The product property of radicals is used to rationalize a
denominator.

Product Property of Radicals
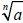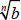If and are real numbers, then .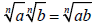
Specifically, if n = 2 and a = b, then

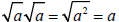
Example 1
 Rationalize a One-Term, Square Root
(n = 2) Denominator

1. Simplify (rationalize the denominator)

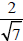
2. Simplify (rationalize the denominator)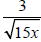
 

Example 2
Rationalize a One-Term, Cube
Root (n = 3) Denominator

Note

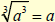1. Simplify (rationalize the denominator)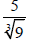

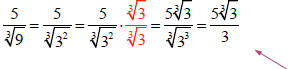	the goal is to make the radicand a perfect cube

2. Simplify (rationalize the denominator)

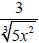
3. Simplify (rationalize the denominator)

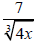
Properties of Radicals

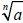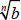If and are real numbers, then

Product Property	Quotient Property

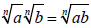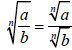Simplified Radical Expression
A radical expression is simplified if
1. There are no radicals in a denominator.
2. There are no fractions inside a radical symbol.
3. All radicands have no nth power factors.
4. The numerator and denominator of any rational
expression (fractions) have no common factors.

Example 3

1. Simplify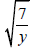

2. Simplify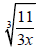

3. Simplify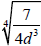

Rationalize a Two-Term Denominator

Conjugate
The conjugate of the two-term expression a + b is a − b
and visa versa.

Example 4
For each of the following, identify the conjugate of the
expression. Then find the product of the expression and its
conjugate.

Expression	Conjugate	Product
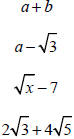	a − b

Fact
The product of a square-root expression and it’s
conjugate is an expression containing no square
roots (i.e. a rational expression).

Example 5

Simplify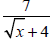
 

Example 6

Simplify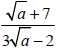

9.5 Solve Square Root Equations

Recall that expressions are things we can be asked to
simplify, add, subtract, multiply, and divide. However,
equations (two equal expressions) are things we are asked
to solve. In this section we will solve square root
equations, such as,

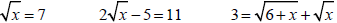
To Solve an Equation Containing One Square
Root Term
1. Isolate the square root term on one side of the equation.
2. Square both sides of the equation and solve.
3. Check the solution(s) in the original equation.

Example 1
1. Solve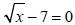

2. Solve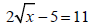

3. Solve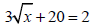

Watch for Extraneous Solutions
When both sides of an equation are squared it is possible
for the modified equation to have a solution that does not
satisfy the given equation - these false solutions are called
extraneous solutions and must be discarded.

Example 2

1. Solve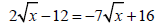

2. Solve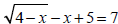

3. Solve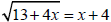

Example 3 Solve each equation.

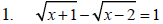
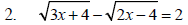
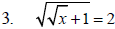
Example 4 Solve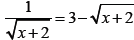

Example 5

1. Find the zeros & x-intercepts of

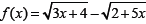
2. Find the y-intercept of f.

3. Verify the results by graphing f on your
calculator.