Solving Radical Equations
Radical Equations
A "radical" equation is an equation in which the variable
is hiding inside
a radical symbol (in the radicand).
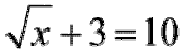
is a radical equation
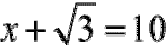
is NOT a radical equation
To solve radical equations:
1. Isolate the radical (or one of the radicals) to one side of the
equal sign.
2. If the radical is a square root, square each side of the
equation. (If the radical is not a square root, raise each side to a
power
equal to the index of the root.)
3. Solve the resulting equation.
4. Check your answer(s) to avoid extraneous roots. |
BEWARE!!
When working with radical equations (that are square
roots), ...
1. you must square sides, not terms. Consider:
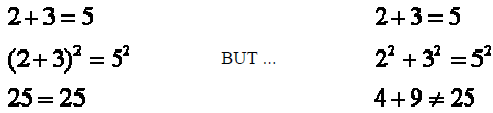
2. you must check your answers. The process of squaring the sides of an
equation creates a
"derived" equation which may not be equivalent to the original radical
equation. Consequently,
solving this new derived equation may create solutions that never
previously existed. These
"extra" roots that are not true solutions of the original radical
equation are called extraneous
roots and are rejected as answers. Consider:
The first statement is false, but
when each side is squared, the
concluding statement is true.
 |
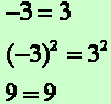The first statement is false, but
when each side is squared, the
concluding statement is true.
 |
|
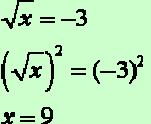Solving Radical Equations
We examine ways to solve equations such as
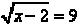. In solving any equation, we
always “undo” the operation so that we can get x isolated. In this case we have
to square
both sides of the equation. The examples cited below describe some of the
methods
needed to solve equations which include radicals.
#1. To solve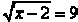 
we first
square both sides of the equation.
The result is x - 2 = 81. This equation is simple to solve. We have x = 83.
#2. A more complicated situation is
.
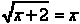In this case we still begin by squaring both sides of the equation. The result
is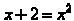 
.
To finish solving this requires us to set all terms equal to zero and either
factor or use the
quadratic formula. We get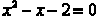 
.
This factors: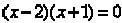
and the solutions are x = 2 or
x = - 1.
We must check each of these solutions in the original
equation to see if the value of x gives
a solution.
x = 2 gives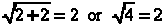 
which is
correct.
x = - 1 gives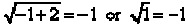 
which is impossible since
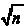for n > 0 is always
positive.
Therefore the only solution is x = 2.
Keeping in mind the basic idea of squaring both sides of the equation in order
to solve for x
when there is a radical in the equation, we will now show some additional
examples.
#3. Solve for x if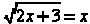 
.
Squaring both sides of the equation gives us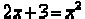 
.
Setting terms equal to zero gives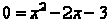 
.
The expression factors: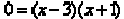 
.
Setting each factor equal to 0 gives two possible answers: x = 3 or x = – 1.
We check each answer in the original equation:
If x = 3 we have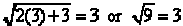
which is correct.
If x = – 1 we have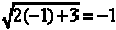 
which is impossible since
the square root cannot be
negative.
Therefore the only answer is x = 3.
#4. Suppose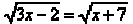 
.
We begin again by squaring both sides of the equation. The result is 3x – 2 = x
+ 7.
We solve for x getting 2x = 9 or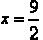 
.
We check this possible answer in the original equation.
If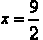 
we have
.
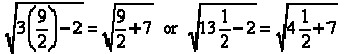This is the same as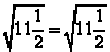 
which is correct.
Therefore the solution is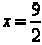 
.
#5. Solve for x if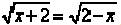 
.
We square both sides. This gives x + 2 = 2 – x.
Solving for x gives 2x = 0. The only solution is x = 0.
Checking this in the original equation gives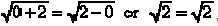 
which is correct.
Therefore the solution is x = 0.
#6. Let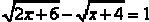 
.
Our first step is to separate the radicals. The result is
.
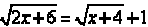Now we square both sides. The result is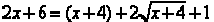 
.
We next isolate the radical term on the right side. The result is
.
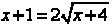We square both sides again. The result is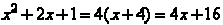 
.
We set the terms equal to zero. The result is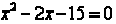 
.
We solve this by factoring or using the quadratic formula. This does factor: (x
– 5)(x + 3) =
0. This gives two possible solutions: x = 5 or x = – 3.
We check these possible solutions in the original equation.
If x = 5 we have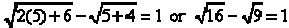 
. This is the same as 4 – 3
= 1.
If x = – 3 we have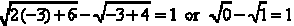 
. This is impossible since
.
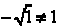Therefore the only solution is x = 5.
