Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Roots of Polynomials

Section I: Linear Polynomials

Consider the polynomial equation ax + b = 0, symbolically solve for the value of x.

Of course the value of x is called the root of the linear polynomial ax + b. The TI-86
has a built in polynomial solver package accessed via 2nd POLY on the key board.
To find the roots of a polynomial using MAPLE we can use the command

solve(our polynomial=0);

Find the roots of the polynomials in each of three ways: first "by hand", then via the
TI-86, and lastly using MAPLE. Record the answers in order left to right.

	P&B	SGC	CAS	Comments

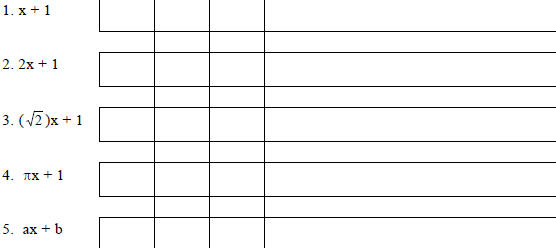Try #5 using the command solve(a*x + b=0, x); in MAPLE.
Why do you think the information ",x" must be put into the MAPLE command in
#5 when we didn't need it in the others?

What conclusion do you make with regard to using the TI-86 directly to solve linear
polynomials?

In using MAPLE in #5 we have encountered our first instance of using the amazing
feature that distinguishes a Computer Algebra System (CAS) from the previous
generation of mathematics software packages: it can do Symbolic Manipulation!

Section II. Quadratic Polynomials

Next let's solve some quadratics; that is, find the roots of polynomials of the form
ax²+bx+c. You have done this once, but do it again. The quadratic formula tells us
the two roots of ax²+bx+c are

x =

and x=

As above, find the roots of the following "by hand", with the TI-86,(it should work
here) and with MAPLE.(Can you guess which problems will require insertion of ,x
into the solve command, and which will not?)

	P&B	SGC	CAS	Comments

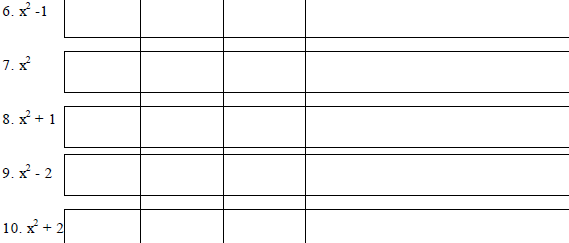What's special about #8 and #10?

Notice the difference in the way the TI-85 expresses complex numbers and the way
MAPLE expresses them.

	P&B	SGC	CAS	Comments

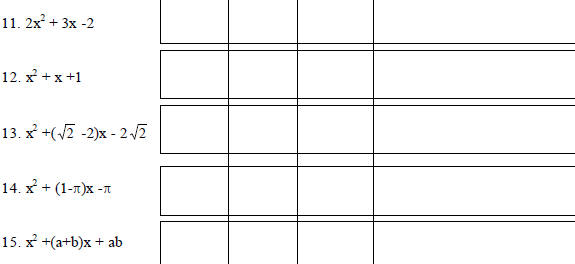Now see what MAPLE gives when you ask it to solve for the roots of
16. ax² + bx +c.

X =

&X =

This should look familiar to you, what is it?

Exercise: In each of the above, 6-15, try to use the evalf command in MAPLE to
obtain the TI-86 approximate answer. You will first need to define something to be
the roots, eg,

r:=expression;

defines r to be whatever is the expression. So

r:=solve(2x²-3x+2=0,x);

represents the two roots of 2x^2-3x+2=0.
Since r represents two roots evalf(r[1]); will evaluate the floating point approximation
to the first root and evalf(r[2]); will approximate the second. So try this for each of
the above. See if you can guess in advance which work and which don't.

MAPLE 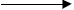Approximation			TI ans
	evalf

Next we will play with two MAPLE commands that further illustrate the nice features
of symbolic manipulation:

expand(algebraic expression); and factor(algebraic expression);
In each of the following first do the required calculation "by hand", then let MAPLE
do it.

by hand		MAPLE
	16. expand((x+3)*(x-4));
	17. factor(%);
	18. factor(2x² +3x -2);
	19. expand((ax+1)*(bx+1));
	20. factor(x² +bx +ax +ab);
	21. expand((x+I)*(x-I));
	22. factor(%);

You should now be able to "build" quadratics with any roots you like using expand
and factor. Make some interesting ones.