Roots of Polynomials
Section I: Linear Polynomials
Consider the polynomial equation ax + b = 0, symbolically solve for the value of
x.

Of course the value of x is called the root of the linear
polynomial ax + b. The TI-86
has a built in polynomial solver package accessed via 2nd POLY on the key
board.
To find the roots of a polynomial using MAPLE we can use the command
solve(our polynomial=0);
Find the roots of the polynomials in each of three ways: first "by hand", then
via the
TI-86, and lastly using MAPLE. Record the answers in order left to right.
| |
P&B |
SGC |
CAS |
Comments |
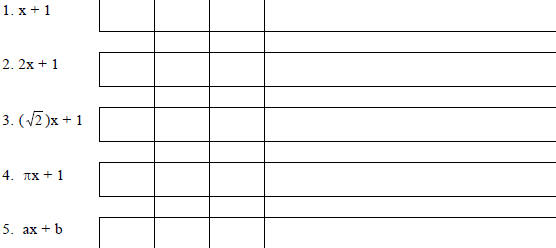 |
Try #5 using the command solve(a*x + b=0, x); in
MAPLE.
Why do you think the information ",x" must be put into the MAPLE command in
#5 when we didn't need it in the others?
What conclusion do you make with regard to using the TI-86
directly to solve linear
polynomials?
In using MAPLE in #5 we have encountered our first
instance of using the amazing
feature that distinguishes a Computer Algebra System (CAS) from the previous
generation of mathematics software packages: it can do Symbolic Manipulation!
Section II. Quadratic Polynomials
Next let's solve some quadratics; that is, find the roots of polynomials of the
form
ax2+bx+c. You have done this once, but do it again. The quadratic formula tells
us
the two roots of ax2+bx+c are
As above, find the roots of the following "by hand", with
the TI-86,(it should work
here) and with MAPLE.(Can you guess which problems will require insertion of ,x
into the solve command, and which will not?)
| |
P&B |
SGC |
CAS |
Comments |
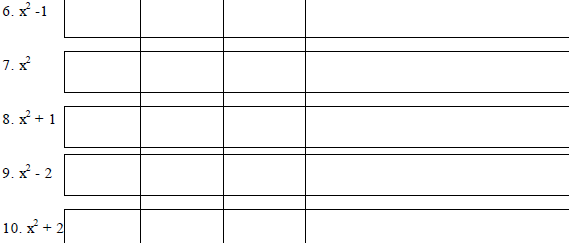 |
What's special about #8 and #10?
Notice the difference in the way the TI-85 expresses
complex numbers and the way
MAPLE expresses them.
| |
P&B |
SGC |
CAS |
Comments |
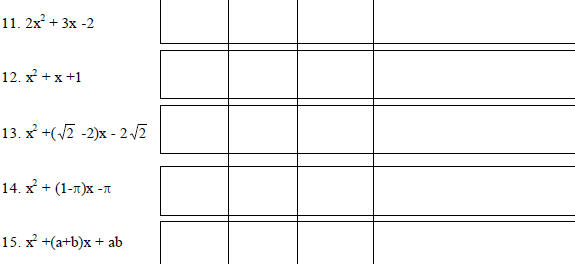 |
Now see what MAPLE gives when you ask it to solve for the
roots of
16. ax2 + bx +c.
This should look familiar to you, what is it?
Exercise: In each of the above, 6-15, try to use the evalf
command in MAPLE to
obtain the TI-86 approximate answer. You will first need to define something to
be
the roots, eg,
r:=expression;
defines r to be whatever is the expression. So
r:=solve(2x2-3x+2=0,x);
represents the two roots of 2x^2-3x+2=0.
Since r represents two roots evalf(r[1]); will evaluate the floating point
approximation
to the first root and evalf(r[2]); will approximate the second. So try this for
each of
the above. See if you can guess in advance which work and which don't.
MAPLE 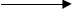 Approximation
Approximation |
TI ans |
| |
evalf |
|
|
Next we will play with two MAPLE commands that further
illustrate the nice features
of symbolic manipulation:
expand(algebraic expression); and factor(algebraic expression);
In each of the following first do the required calculation "by hand", then let
MAPLE
do it.
| by hand |
|
MAPLE |
 |
16. expand((x+3)*(x-4)); |
 |
 |
17. factor(%); |
 |
 |
18. factor(2x2 +3x -2); |
 |
 |
19. expand((ax+1)*(bx+1)); |
 |
 |
20. factor(x2 +bx +ax +ab); |
 |
 |
21. expand((x+I)*(x-I)); |
 |
 |
22. factor(%); |
 |
You should now be able to "build" quadratics with any
roots you like using expand
and factor. Make some interesting ones.