Roots of Quadratic Equations

I. Finding Roots of Quadratic Equations
a. The Standard Form of a quadratic equation is: ax² + bx + c = 0 .
b. We can use the Quadratic Formula to solve equations in standard
form:

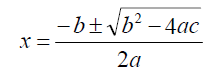
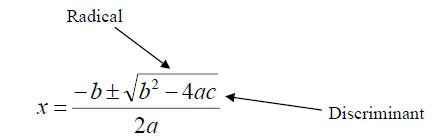
c. Discriminant – The radical portion of this formula sqrt(b² − 4ac) ,
determines the nature of the roots. This quantity under the radical
sign b² − 4ac , is called the discriminant.

d. Three things may occur regarding the discriminant:

i. If b² − 4ac > 0
We can take the square root of this positive amount
and there will be two different real answers (or roots)
to the equation.

ii. If b² − 4ac < 0
We cannot take the square root of a negative number,
so there will be no real roots.

iii. If b² − 4ac = 0
The amount under the radical is zero and since the
square root of zero is zero, we will get only 1 distinct
real root.

II. Examples

III. Practice Problems
By examining the discriminant = b² − 4ac , determine how many real
roots, if any, the following quadratic equations have.

1. x² − 4x + 4 = 0

2. x² + 4 = 0

3. x² − 2x + 4 = 0

4. x² − 4x = 0

5. 5r² − 3r + 2 = 0

6. 7x² −10x − 5 = 0

7. x² − 4 = 0

8. 25t² −10t = −1

9. 6y² − 5y = 21

10. 2y² −19y = 3

Answers: Roots of Quadratic Equations
1. 1 real root
2. no real roots
3. no real roots
4. 2 real roots
5. no real roots
6. 2 real roots
7. 2 real roots
8. 1 real root
9. 2 real roots
10. 2 real roots