Rational Exponents and Radicals Definitions
Defintion 1: If x ≠ 0, then
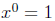 and
and  is
undefined
is
undefined
Defintion 2: If x ≠ 0, then
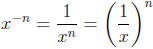 for any rational number n
for any rational number n
For any positive integer n and m
Defintion 3: If n is odd, then “nth root of a” is
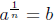 such that
such that
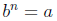
If n is even and a > 0, then “principal nth root of a” is
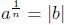 such that
such that
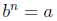
Defintion 4: If
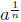 is real, then
is real, then
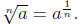
So, for odd n:
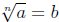 such that
such that
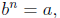 for even n and a > 0:
for even n and a > 0:
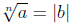 such that
such that
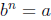
So, for odd n:
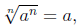 for even n:
for even n:
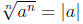 for any a.
for any a.
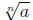 is is
|
not a real number |
if n is even and a < 0 |
| |
a rational number |
if a is a perfect nth power (e.g. 9 = 32 is a perfect square) |
| |
an irrational number |
if a is not a perfect nth power |
Defintion 5: If 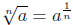 is real, then
is real, then 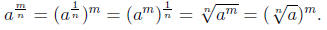
Defintion 6: If 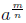 is real, then
is real, then 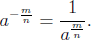
From now on r and s are any rational numbers, m, n
and k are any intergers.
Rules
Rule 1:
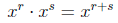
Rule 2:
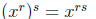
Rule 3:
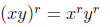
Rule 4: For
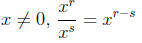
Rule 5: For
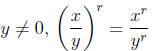
If 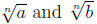 are real then
Rule 6:
are real then
Rule 6: 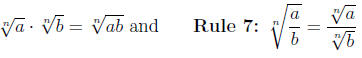
If all indicated roots are real then
Rule 8: 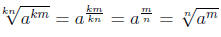
Sumplifying Radicals - Rationalizing denominator
(square roots only!)
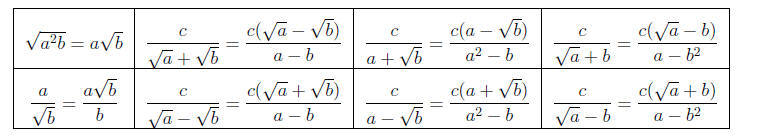
Simplifying Radicals - We will simplify
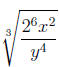 in each step as example.
in each step as example.
Step 1: Rewrite the expression with fractional
exponents/powers.
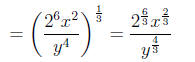 By Rules 2, 3 and 5
By Rules 2, 3 and 5
Step 2: Reduce fractional powers
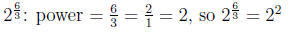
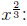 power = 2/3 - already
reduced
power = 2/3 - already
reduced
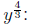 power = 4/3 - already
reduced
power = 4/3 - already
reduced
Step 3: If fractional power > 1, write it as a
mixed fraction, follow example steps.
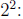 power = 2 - not
fractional power
power = 2 - not
fractional power
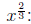 power = 2/3 < 1
power = 2/3 < 1
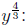 power =
power =
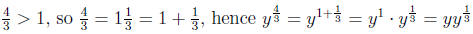
Step 4: Put things back in the main problem
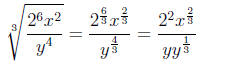
Step 5: Pull out factors with integer powers
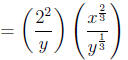
Step 6: Rationalize the denomenator of the 2nd
factor
Denomenator 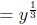 , we need to
make it
, we need to
make it 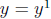 , so multiply numerator by
, so multiply numerator by
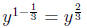
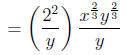 [We get
[We get
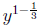 by solving
by solving
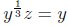 for z]
for z]
Step 7: Pull out the common denomenator of the
fractional power as 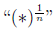
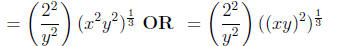
Step 8: Switch back to radical notation
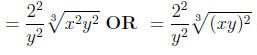 —– Now it is fully
simplified!
—– Now it is fully
simplified!